# 二进制
# 什么是2进制
逢2进1的计数规则(重要)
2进制 规则:逢2进1 数字:0 1 权:128 64 32 16 8 4 2 1 基数:2
10进制计数规则
10进制 规则:逢10进1 数字:0 1 2 3 4 5 6 7 8 9 权:万 千 百 十 个 基数:10
计算机为啥是2进制?便宜!!!成本优势明显!!!
如何将2进制转换为10进制:将1位置对应权值累加求和
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000001 = 1
00000000 00000000 00000000 00000010 = 2
00000000 00000000 00000000 00000011 = 2+1 = 3
00000000 00000000 00000000 00000100 = 4
00000000 00000000 00000000 00000101 = 4+1 = 5
00000000 00000000 00000000 00000110 = 4+2 = 6
00000000 00000000 00000000 00000111 = 4+2+1=7
00000000 00000000 00000000 00001000 = 8
00000000 00000000 00000000 00001001 = 8+1=9
00000000 00000000 00000000 00001010 = 8+2=10
00000000 00000000 00000000 00001011 = 8+2+1=11
00000000 00000000 00000000 00001100
00000000 00000000 00000000 00001101
00000000 00000000 00000000 00001110
00000000 00000000 00000000 00001111
00000000 00000000 00000000 00010000
...
00000000 00000000 00000000 00011001 = 16+8+1=25
...
00000000 00000000 00000000 01101000 = 64+32+8=104
...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
package binary;
public class Demo01 {
public static void main(String[] args) {
/*
* 如何查看整数的2进制存储情况
* - java 编译时候,将10进制数字编译为2进制数字
.java(50)-----------编译后----------.class(110010)
* - 运行期间变量中存储的是2进制数
* - 输出变量时候,Java利用API方法,将2进制转换为10进制字符串
* 利用valueOf方法转换!
* - Integer.toBinaryString(n) 将整数n在内存中2进制情况显示出来
int类型是32位2进制数,显示2进制时自动省略高位0
*/
int n = 50; //n=110010
System.out.println(n); //利用valueOf转换2进制为10进制字符串输出
System.out.println(Integer.toBinaryString(n));
System.out.println(Integer.toBinaryString(104));
/*
* 输出0~200的2进制, 手工计算20个数的10进制值,编程验证
*/
for(int i=0; i<200; i++){
System.out.println(Integer.toBinaryString(i));
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 什么是16进制
逢16进1的计数规则。
16进制用途:16进制用于缩写2进制。
- 2进制书写非常繁琐
- 16进制的基数是2进制的基数4次方, 2进制每4位数可以缩写为1个16进制数。
- 权:4096 256 16 1
package binary;
public class Demo02 {
public static void main(String[] args) {
/*
* 2进制与16进制
* - Java7 提供了2进制字面量前缀 0b---------一般不用
* 可以在数字中添加下划线,不影响数值
* - 2进制直接书写非常繁琐
* - 16进制缩写2进制就非常方便
* 从2进制的最低位开始, 每4位数缩写为1位16进制数
* - 0x是16进制的前缀
* - 计算内部没有10进制,没有16进制,只有2进制!
* - 以0开头表示8进制
*/
int n = 0b11_0010;//32+16+2=50
System.out.println(n);
n = 0b0001_1001_1111_0001_0100_0011_1111_0101;
// 1 9 f 1 4 3 f 5
System.out.println(Integer.toBinaryString(n));
n = 0x19f143f5;
System.out.println(Integer.toBinaryString(n));
long l = 0b10111111111111111111111111111111111111L;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 补码
计算中一种表示有符号数编码,其核心思想就是将固定位数2进制分一般作为负数,(0在计算机中也算是正数).
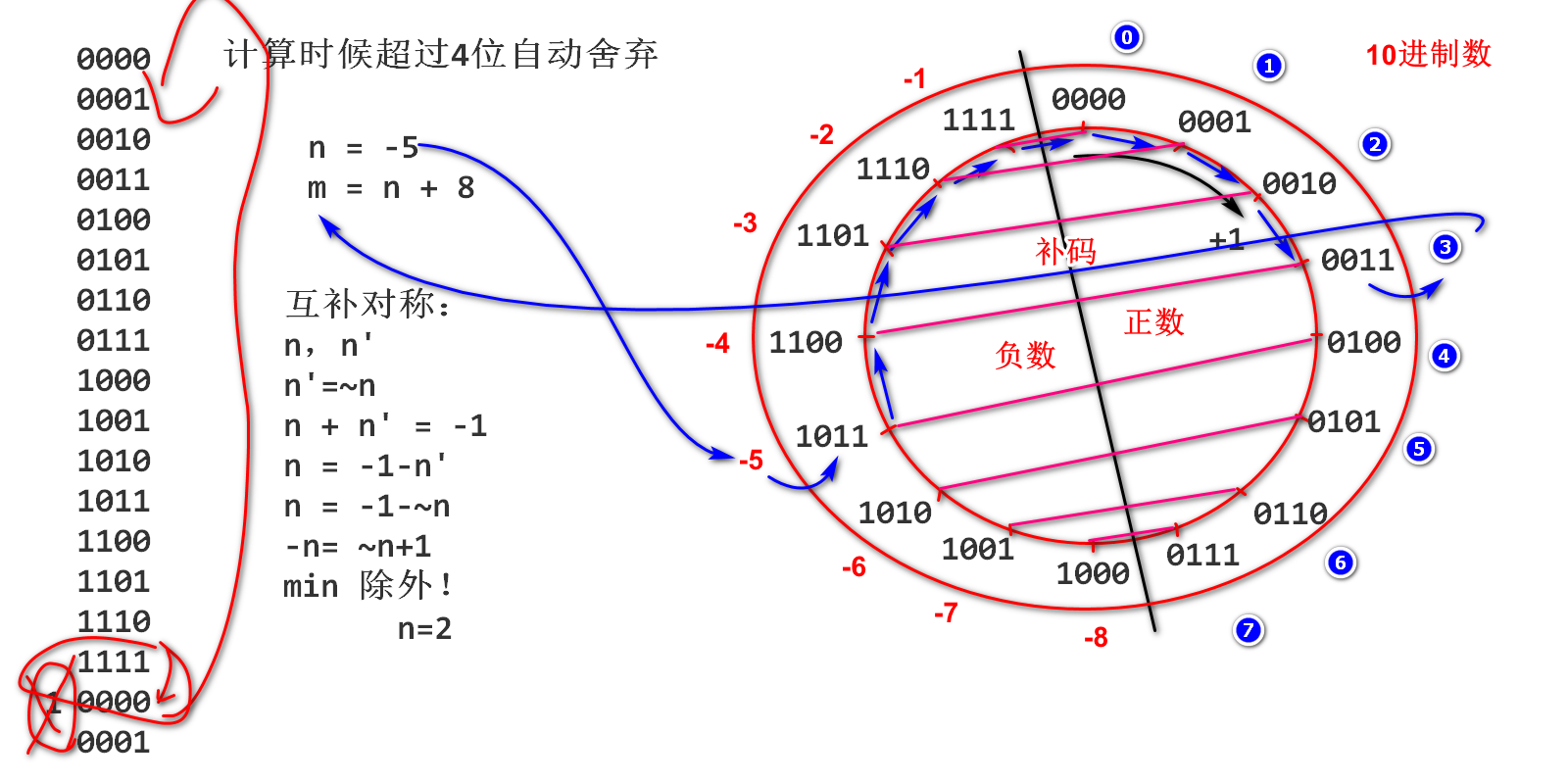
Java中的补码最小类型是int,32位数.
如何将固定位数2进制分一半作为负数?
以4位2进制数讲解如何设计补码
计算时候保持4位不变, 如果超出4位数就自动溢出舍弃.
最高位称为符号位,0是正数,1是负数
将4位2进制数分一半作为负数使用
最高位称为符号位,高位为1是负数,高位为0是正数
# 规律数
- 0111为4位补码的最大值,规律是1个0和3个1,可以推导出:--32位补码的最大值:是1个0和31个1--------(01111111111...)
- 1000为4位补码的最小值,规律是1个1和3个0,可以推导出:--32位补码的最小值:是1个1和31个0--------(10000000000...)
- 1111为4位补码的-1,规律是4个1,可以推导出:--32位补码的-1:是32个1------------(111111111111...)
package binary;
public class Demo03 {
public static void main(String[] args) {
/*
* 补码
* max 最大
* value 值
* Integer 整数
*/
int n = -3;
System.out.println(Integer.toBinaryString(n));
int max = Integer.MAX_VALUE;
int min = Integer.MIN_VALUE;
System.out.println(max);
System.out.println(min);
System.out.println(Integer.toBinaryString(max));
System.out.println(Integer.toBinaryString(min));
System.out.println(Integer.toBinaryString(-1));
System.out.println(Long.toBinaryString(-1L));
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
手工计算负数的值: 计算这个数比-1少0位置的权。
11111111111111111111111111111111 = -1
11111111111111111111111111111101 = -1-2=-3
11111111111111111111111111111001 = -1-2-4=-7
11111111111111111111111111111000 = -1-1-2-4=-8
11111111111111111111111101101011 = -1-4-16-128=-149
11111111111111111111111101101100 = -1-1-2-16-128=-148
1
2
3
4
5
6
2
3
4
5
6
package binary;
public class Demo04 {
public static void main(String[] args) {
/*
* 负数的编码
* 实验: 输出-200到0的2进制编码(补码)
* 随机选取20个数,手动计算10进制值
* 利用Java程序验算计算结果。
*/
for(int i=-200; i<0; i++){
System.out.println(Integer.toBinaryString(i));
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
15
long类型负数补码
1111111111111111111111111111111111111111111111111111111111111111 = -1
1111111111111111111111111111111111111111111111111111111111100110 =-26
1
2
2
互补对称现象:-n = ~n+1
-7 = 11111111 11111111 11111111 11111001 = -1-2-4=-7
~-7 = 00000000 00000000 00000000 00000110 = 2+4 = 6
~-7+1 = 00000000 00000000 00000000 00000111 = 1+2+4=7
54 =00000000 00000000 00000000 00110110= 2+4+16+32=54
~54 =11111111 11111111 11111111 11001001=-1-2-4-16-32=-55
~54+1 =11111111 11111111 11111111 11001010=-1-1-4-16-32=-54
1
2
3
4
5
6
7
2
3
4
5
6
7
代码:
public class Demo05 {
public static void main(String[] args) {
/*
* 验证补码的互补对称现象 -n=~n+1
*/
System.out.println(54);
System.out.println(Integer.toBinaryString(54));
System.out.println(~54);
System.out.println(Integer.toBinaryString(~54));
System.out.println(~54+1);
System.out.println(Integer.toBinaryString(~54+1));
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
2
3
4
5
6
7
8
9
10
11
12
13
# 2进制运算
运算符号:
~ 取反
& 与
| 或运算
>>> 右移位运算
>> 数学右移位运算
<< 左移位运算
1
2
3
4
5
6
2
3
4
5
6
# & 与运算
运算规则:逻辑乘法 有0则0
0 & 0 -> 0
0 & 1 -> 0
1 & 0 -> 0
1 & 1 -> 1
1
2
3
4
2
3
4
运算时候将两个2进制数对其位,对应位置进行与运算
栗子:
1 7 9 d 5 d 9 e
n = 00010111 10011101 01011101 10011110
m = 00000000 00000000 00000000 11111111 8位掩码
k=n&m 00000000 00000000 00000000 10011110
1
2
3
4
2
3
4
如上运算的意义:k中存储的是n的最后8位数,如上运算叫掩码(mask)运算。m称为mask(掩码),一般从低位开始1的个数称为掩码的位数。
代码:
int n = 0x179d5d9e;
int m = 0xff;
int k = n & m;
1
2
3
2
3
package binary;
import java.util.ArrayList;
public class Demo06 {
public static void main(String[] args) {
/*
* 掩码运算
*/
int n = 0x179d5d9e;
//4位掩码:0xf 0b1111 15
//6位掩码:0x3f 0b111111 63
//8位掩码:0xff 0b11111111 255
int m = 0xff; //4位 6位 8位 16位
int k = n & m;
System.out.println(Integer.toBinaryString(n));
System.out.println(Integer.toBinaryString(m));
System.out.println(Integer.toBinaryString(k));
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# >>> 右移位运算
运算规则, 将2进制数整体向右移动,低位自动溢出舍弃,高位补0
n = 01100111 11010111 10001111 01101101
m=n>>>1 001100111 11010111 10001111 0110110
k=n>>>2 0001100111 11010111 10001111 011011
g=n>>>8 00000000 01100111 11010111 10001111
b3 = (n>>>8) & 0xff;
1
2
3
4
5
2
3
4
5
代码:
int n = 0x67d78f6d;
int m = n>>>1;
int k = n>>>2;
int g = n>>>8;
int b3 = (n>>>8) & 0xff;
//按照2进制输出 n m k g b3
1
2
3
4
5
6
2
3
4
5
6
# | 或运算
基本运算规则:逻辑加法, 有1则1
0 | 0 -> 0
0 | 1 -> 1
1 | 0 -> 1
1 | 1 -> 1
1
2
3
4
2
3
4
运算时候两个2进制数对齐位,对应位进行或运算
栗子:
n = 00000000 00000000 00000000 11011101
m = 00000000 00000000 10011101 00000000
k=n|m 00000000 00000000 10011101 11011101
1
2
3
2
3
上述计算的意义: 两数错位合并
代码:
int n = 0xdd;
int m = 0x9d00;
int k = n | m;
//检查 n m k 的2进制
1
2
3
4
2
3
4
# << 左移位运算
2进制数字整体向左移动,高位自动溢出,低位补0
栗子:
n = 00100000 11101111 00110101 10010000
m=n<<1 0100000 11101111 00110101 100100000
k=n<<2 100000 11101111 00110101 1001000000
g=n<<8 11101111 00110101 10010000 00000000
1
2
3
4
2
3
4
代码:
int n = 0x20ef3590;
int m = n<<1;
int k = n<<2;
int g = n<<8;
//按照2进制输出 n m k g
1
2
3
4
5
2
3
4
5
# 移位运算的数学意义
栗子:
16 8 4 2 1
1 0 1 = 5
1 0 1 = 10 向左移动1位 *2
1 0 1 = 20 向左移动2位 *2*2
1
2
3
4
2
3
4
代码:
int n = 5;
System.out.println(n<<1); //10
System.out.println(n<<2); //20
System.out.println(n<<3); //40
//...
1
2
3
4
5
2
3
4
5
# >>> 和 >> 的区别
>>>逻辑右移位:数字向右移动,低位自动溢出,高位补0, 结果没有数学意义。如果仅仅将数位向右移动,不考虑数学意义,则使用>>>>>数学右移位:数学向右移动,低位自动溢出,正数高位补0,负数高位补1, 移动一次数学除以2,小方向取整数。如果是替代数学 /2, 使用数学右移位。
栗子, 使用负数比较运算结果:
n = 11111111 11111111 11111111 11001100=-1-1-2-16-32=-52
m=n>>1 111111111 11111111 11111111 1100110=-1-1-8-16=-26
k=n>>2 1111111111 11111111 11111111 110011=-1-4-8=-13
g=n>>3 11111111111 11111111 11111111 11001=-1-2-4=-7
n>>>1 011111111 11111111 11111111 1100110=max-25没有数学意义
1
2
3
4
5
2
3
4
5
程序:
int n = -52; //0xffffffcc;
int m = n>>1;
int k = n>>2;
int g = n>>3;
int x = n>>>1;
//输出n m k g x
1
2
3
4
5
6
2
3
4
5
6
# 将一个整数拆分为4个字节
栗子
b1 b2 b3 b4
n = 00010111 10011101 01011101 10011110
b1 = 00000000 00000000 00000000 00010111
b2 = 00000000 00000000 00000000 10011101
b3 = 00000000 00000000 00000000 01011101
b4 = 00000000 00000000 00000000 10011110
1
2
3
4
5
6
2
3
4
5
6
代码:n =-1 n=-3 n=max n=min
int n = 0x179d5d9e;
int b1 = (n >>> 24) & 0xff;
int b2 = (n >>> 16) & 0xff;
int b3 = (n >>> 8) & 0xff;
int b4 = n & 0xff;
//验证:按照二进制输出 n b1 b2 b3 b4
//n=-1 时候按照10进制输出是啥结果?
1
2
3
4
5
6
7
2
3
4
5
6
7
# 将4个字节合并为一个整数
b1 = 00000000 00000000 00000000 00010111
b2 = 00000000 00000000 00000000 10011101
b3 = 00000000 00000000 00000000 01011101
b4 = 00000000 00000000 00000000 10011110
b1<<24 00010111 00000000 00000000 00000000
b2<<16 00000000 10011101 00000000 00000000
b3<<8 00000000 00000000 01011101 00000000
b4 00000000 00000000 00000000 10011110
n = (b1<<24) | (b2<<16) | (b3<<8) | b4;
1
2
3
4
5
6
7
8
9
10
11
2
3
4
5
6
7
8
9
10
11
代码:
int b1 = 0x17;
int b2 = 0x9d;
int b3 = 0x5d;
int b4 = 0x9e;
int n = (b1<<24) | (b2<<16) | (b3<<8) | b4;
//按照2进制输出 b1 b2 b3 b3 n
1
2
3
4
5
6
2
3
4
5
6